[DB] b-tree, b+tree

B-tree란?

• Balanced-Tree
• 균형 트리로 루트로부터 리프까지의 거리가 일정한 트리 구조
• 이렇게 균형을 유지할 경우 어떤 데이터를 검색할 때 빠른 속도로 데이터 검색 가능
• 00차 트리 → 최대 자식수가 00개

B-트리의 특징

• B트리는 이진트리와 다르게 하나의 노드에 많은 수의 정보를 가질 수 있습니다. 최대 M개의 자식을 가질 수 있는 B-트리를 M차 B-트리라고 합니다.
  • 노드는 최대 M개의 자식 노드를 가질 수 있다.
  • ex) 3차 B-트리라면 최대 3개의 자식 노드를 가질 수 있다.
  • 노드에는 최대 M-1개의 KEY를 가질 수 있다.
  • ex) 3차 B-트리라면 최대 2개의 KEY를 가질 수 있다.
  • 각 노드는 최소 M/2개의 자식 노드를 가진다. (루트 노드와 leaf 노드 제외)
  • ex) 3차 B-트리라면 각 노드는 최소 2개의 자식 노드를 가진다.
  • 각 노드는 최소 M/2-1개의 키를 가진다. (루트 노드 제외)
  • ex) 3차 B-트리라면 각 노드는 최소 1개의 키를 가진다.
  • internal 노드의 KEY가 x개라면 자녀 노드의 수는 언제나 x+1 개다.
  • 노드가 최소 하나의 KEY는 가지기 때문에 몇 차 인지에 상관없이 internal 노드는 최소 두개의 자녀는 가진다.
  • 노드에 KEY들은 항상 정렬된 상태로 저장된다.

단점

• 만약 트리의 노드가 수정되어야 한다면 재정렬을 해줘야 하기 때문에 수정시 불리
• insert, delete등이 힘들어진다.
  • ex)분할이 일어나지 않는 경우

    • 

     
  • ex)분할이 일어나는 경우

    • 

     

• 가장 큰 단점은 바로 시퀀셜 액세스에 취약하다는 점.
  • 데이터를 가져올 때 range를 정해놓고 속하는 데이터를 가져오는 작업에서는 어려움
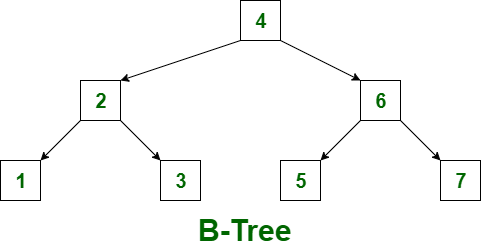
  • 아래와 같은 구조에서 데이터 액세스를 시도한다면, 기본적으로 B-Tree는 루트부터 하향식으로 데이터를 찾아가기 때문에 복잡해짐. 게다가 실제 데이터는 입력 순서대로 저장되어 있지도 않기 때문에 이렇게 흩뿌려져 있는 데이터를 정렬된 형태로 보여주는 작업은 매우 복잡합니다.
   

B+tree

• **리프 노드를 제외하고 값을 담아두지 않기 때문에 하나의 블록에 더많은 Key 들을 담아 둘 수 있다(**트리의 높이가 낮아짐)
• 풀 스캔시 B+Tree는 리프 노드에 데이터가 모두 있기 때문에 한번의 선형 탐색만 하면 되기 때문에 B-Tree 에 비해 빠르다
• 같은 레벨의 노드에서는 Double Linked List 를 사용하고 자식 노드는 Single Linked List 를 사용합니다.

• b-트리의 단점이던 시퀀셜 액세스도 무난함

B-tree와 B+tree의 비교

	B-tree	B+tree
주요 특징	모든 내부, 리프 노드들이 데이터를 가진다	단지 리프노드만 데이터를 가진다
검색	모든 키가 리프에서 사용가능 하지 않기 때문에, *검색이 때로 느리다	모든 키가 리프 노드에 있기 때문에 검색이 빠르고 정확하다
중복 키	트리에 중복키가 없다	중복키가 존재하며 모든 데이터들은 리프에 있다
삭제	내부 노드의 삭제는 목잡하고 트리 변형이 많다	어떠한 노드든 리프에 있기 때문에 삭제가 쉽다
리프노드	링크드 리스트로 저장되지 않는다	링크드 리스트로 저장된다
높이	특정 갯수의 노드는 높이가 높다	같은 노드일 때 B-tree보다 높이가 낮다
사용	데이터베이스, 검색엔진	멀티레벨 인덱스, DB 인덱스

*검색에 대한 부가설명

• 적은 양을 찾기에는 b-tree가 빠르고
• 연속적인 데이터, 즉 시퀀셜 데이터를 찾을때는 b+tree가 빠르다고 이해함